Задача про фрукты

 ЗАДАЧИ  НА  СУШЕНЫЕ ФРУКТЫ.

23.3-7.Свежие фрукты содержат 86% воды, а высушенные — 23%. Сколько сухих фруктов получится из 341 кг свежих фруктов?

 Решение. При решении подобных задач следует определить ту величину, которая не меняется при высыхании (уменьшении влажности). Неизменной в данных процессах остается масса сухого вещества, т. е. продукта, в котором полностью отсутствует вода.

 Если 341 кг фруктов имеют влажность 86 %, то жидкость составляет 341 × 0,86 = 293,26 кг, а сухое вещество имеет массу 341- 293,26 = 47,74 кг.

 Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 23 % воды, сухое вещество составляет 77 %. Следовательно,

47,74кг——77%

 Х кг – 100 %

откуда Х= 47,74∙100/ 77 = 62кг.

 Ответ: из 341 кг свежих фруктов получится 62 кг сухих.

55.3-В7—Свежие фрукты содержат 78% воды, а высушенные — 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?

 РЕШЕНИЕ: Если 78 кг фруктов имеют влажность 78 %, то жидкость составляет 78 × 0,78 = 60,84 кг, а сухое вещество имеет массу 78 – 60,84 = 17,16кг.

 Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 22 % воды, сухое вещество составляет 78 %.

 Следовательно, 17,16кг——78%

                                  Х кг – 100 % откуда Х= 17,16∙100: 78 = 22кг. Ответ: из 78 кг свежих фруктов получится 22 кг сухих.

 66.3-9 Свежие фрукты содержат 79% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?

 РЕШЕНИЕ:

 х кг = свежих фруктов 100%-79%=21% — сухого вещества в свежих фруктах 100%-16%=84% — сухого вещества в сухих фруктах

 Уравнение: 0,21х=72*0,84 х=288 х=288(кг) — надо взять свежих фруктов

 87.3-12. Свежие фрукты содержат 89% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 84 кг высушенных фруктов?

 РЕШЕНИЕ: х кг = свежих фруктов 100%-89%=11% — сухого вещества в свежих фруктах 100%-23%=77% — сухого вещества в сухих фруктах Уравнение: 0,11х=84*0,77 х=588 х=588(кг) — надо взять свежих фруктов

 215.3.42. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?

РЕШЕНИЕ: При решении подобных задач следует определить ту величину, которая не меняется при высыхании (уменьшении влажности). Неизменной в данных процессах остается масса сухого вещества, т. е. продукта, в котором полностью отсутствует вода. Если 288 кг фруктов имеют влажность 80 %, то жидкость составляет 288 × 0,8 = 230,4кг, а сухое вещество имеет массу 288 — 230,4 = 57,6 кг. Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 28 % воды, сухое вещество составляет 74 %. Следовательно, 57,6——74%

                                     Х кг – 100 % откуда Х= 57,6∙100 74 = 7кг. Ответ: из 20 кг свежих фруктов получится 7 кг сухих.

 216.Задача 5.Свежие фрукты содержат 72 % воды, а сухие – 20 % воды. Сколько сухих фруктов получится из 20 кг свежих?

 Решение. При решении подобных задач следует определить ту величину, которая не меняется при высыхании (уменьшении влажности). Неизменной в данных процессах остается масса сухого вещества, т. е. продукта, в котором полностью отсутствует вода. Если 20 кг фруктов имеют влажность 72 %, то жидкость составляет 20 × 0,72 = 14,4 кг, а сухое вещество имеет массу 20 – 14,4 = 5,6 кг. Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 20 % воды, сухое вещество составляет 80 %. Следовательно, 5,6 кг являются 0,8 частью от общей массы сухих фруктов, а вся масса равняется 5,6 0,8 = 7кг.Можно было получить результат, составив пропорцию 5,6 кг- 80 %

                                                             Х кг – 100 % откуда Х= 5,6∙100 80 = 7кг. Ответ: из 20 кг свежих фруктов получится 7 кг сухих.

433.3.80( 1). Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько требуется свежих фруктов для приготовления 80 кг высушенных фруктов?

 РЕШЕНИЕ: х кг = свежих фруктов 100%-80%=20% — сухого вещества в свежих фруктах 100%-28%=72% — сухого вещества в сухих фруктах Уравнение: 0,2х=0,72*80 0,2х=57,6 х=57,6:0,2 х=288(кг) — надо взять свежих фруктов

 ІІ способ: 100%-80%=20% — сухого вещества в свежих фруктах 100%-28%=72% — сухого вещества в сухих фруктах 80кг-100% ?кг — 72% 80*72:100=288/5(кг) — сухого вещества в сухих фруктах, что составляет 20% в свежих 288/5 кг — 20% ?кг — 100% 288/5*100:20=288(кг)

434.3.80(2 ). Свежие фрукты содержат 78% воды, а высушенные — 22%. Сколько требуется свежих фруктов для приготовления 22 кг высушенных фруктов?

 РЕШЕНИЕ: х кг = свежих фруктов 100%-78%=22% — сухого вещества в свежих фруктах 100%-22%=78% — сухого вещества в сухих фруктах Уравнение: 0,22х=22*0,78 х=78 х=78(кг) — надо взять свежих фруктов

 435 3.80(3 ). Свежие фрукты содержат 75% воды, а высушенные — 25%. Сколько требуется свежих фруктов для приготовления 45 кг высушенных фруктов?

 РЕШЕНИЕ: х кг = свежих фруктов 100%-75%=25% — сухого вещества в свежих фруктах 100%-25%=75% — сухого вещества в сухих фруктах Уравнение: 0,25х=45*0,75 х=135 х=135(кг) — надо взять свежих фруктов

 436.3.80(4 ). Свежие фрукты содержат 79% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?

 РЕШЕНИЕ: х кг = свежих фруктов 100%-79%=21% — сухого вещества в свежих фруктах 100%-16%=84% — сухого вещества в сухих фруктах Уравнение: 0,21х=72*0,84 х=288 х=288(кг) — надо взять свежих фруктов

 437.3.80(5 ). Свежие фрукты содержат 89% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 23 кг высушенных фруктов?

 РЕШЕНИЕ: х кг = свежих фруктов 100%-79%=21% — сухого вещества в свежих фруктах 100%-16%=84% — сухого вещества в сухих фруктах Уравнение: 0,21х=72*0,84 х=288 х=288(кг) — надо взять свежих фруктов

 438.3.80(6 ). Свежие фрукты содержат 95% воды, а высушенные — 22%. Сколько требуется свежих фруктов для приготовления 55 кг высушенных фруктов?

 РЕШЕНИЕ: х кг = свежих фруктов 100%-95%=5% — сухого вещества в свежих фруктах 100%-22%=78% — сухого вещества в сухих фруктах Уравнение: 0,05х=55*0,78 х=858 х=858(кг) — надо взять свежих фруктов

 439. 3.80(7 ). Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 21 кг высушенных фруктов? ОТВЕТ:259

 440.3.80(8 ). Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов? ОТВЕТ:35

 441.3.80( 9). Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов? ОТВЕТ:420

 442.3.80( 10). Свежие фрукты содержат 84% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 44 кг высушенных фруктов? ОТВЕТ:231

 443.3.80(11 ). Свежие фрукты содержат 86% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 94 кг высушенных фруктов? ОТВЕТ:470

444.3.80(12 ). Свежие фрукты содержат 72% воды, а высушенные — 26%. Сколько требуется свежих фруктов для приготовления 84 кг высушенных фруктов? ОТВЕТ:222

445.3.80(13 ). Свежие фрукты содержат 84% воды, а высушенные — 17%. Сколько требуется свежих фруктов для приготовления 16 кг высушенных фруктов? ОТВЕТ:83

 446. 3.80(14 ). Свежие фрукты содержат 86% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов? ОТВЕТ:396

 447.3.80( 15). Свежие фрукты содержат 89% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 84 кг высушенных фруктов? ОТВЕТ:588

 448.3.80(16 ). Свежие фрукты содержат 81% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 95 кг высушенных фруктов? ОТВЕТ:420

 449.3.80( 17). Свежие фрукты содержат 91% воды, а высушенные — 19%. Сколько требуется свежих фруктов для приготовления 84 кг высушенных фруктов? ОТВЕТ:756

 450. 3.80(18 ). Свежие фрукты содержат 85% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 75 кг высушенных фруктов? ОТВЕТ:420

 451.3.80( 19). Свежие фрукты содержат 90% воды, а высушенные — 24%. Сколько требуется свежих фруктов для приготовления 90 кг высушенных фруктов? ОТВЕТ:684

 452. 3.80(20 ). Свежие фрукты содержат 86% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 62 кг высушенных фруктов? ОТВЕТ:341

 525.Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 54 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

 РЕШЕНИЕ: Пусть Х кг. взяли винограда. Виноград содержит 90% воды, а сухого вещества 10%, изюм содержит 5% воды, а сухого 95%, тогда сухого в изюме 54∙ 0,95, а в винограде 0,1 ∙ Х, отсюда уравнение 54∙ 0,95 =0,1∙ Х, Х = 513. ОТВЕТ: 513

526. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 42 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

 РЕШЕНИЕ: Пусть Х кг. взяли винограда. Виноград содержит 90% воды, а сухого вещества 10%, изюм содержит 5% воды, а сухого 95%, тогда сухого в изюме 42∙ 0,95, а в винограде 0,1 ∙ Х, отсюда уравнение 42∙ 0,95 =0,1∙ Х, Х = 399. ОТВЕТ: 399

 527. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 58 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

 РЕШЕНИЕ: Пусть Х кг. взяли винограда. Виноград содержит 90% воды, а сухого вещества 10%, изюм содержит 5% воды, а сухого 95%, тогда сухого в изюме 58∙ 0,95, а в винограде 0,1 ∙ Х, отсюда уравнение 58∙ 0,95 =0,1∙ Х, Х = 399. ОТВЕТ: 399

 541.10.B 14 № 99574. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма? Решение В винограде-ВОДЫ-90%, СУХОГО-10%. Пусть Х кг нужно взять винограда, а сухого в нем 0,1Х. В изюме – воды 5%, сухого-95%. Изюма нужно получить 20 кг, а сухого в нем будет 0,95∙ 20 Отсюда уравнение 0,1Х.= 0,95∙ 20, Х=190. Ответ: 19

Предварительный просмотр:

Задачи на движение с учётом длины объектов.

В задачах на движение протяжных тел требуется определить длину одного из них, или учесть его длину при нахождении компонент движения.  Можно выделить основные виды таких задач. Это – определение длины поезда проезжающего

• мимо точечного объекта – стрелочник, семафор, придорожный столб;
• мимо длинного объекта – платформа, мост, туннель, лесополоса;
• мимо идущего пешехода ( навстречу или в том же направлении);
• мимо движущегося длинного объекта – поезд, баржа.

Лучше всего решать такие задачи с помощью схем, где длинный объект изображается вектором (стрелкой). И полезно помнить, что все точки длинного объекта (поезда) движутся с одинаковой скоростью – со скоростью поезда. Поэтому достаточно для себя выбрать одну из них ( например, крайнюю правую – «нос» объекта) и решать задачу, как задачу на движение именно этой точки.

Рассмотрим на конкретных задачах.

Поезд, двигаясь равномерно со скоростью 84 км/ч, проезжает мимо семафора  за 24 секунды. Найти длину поезда в метрах.

«Мимо семафора  за 24 сек» — это время от момента, когда со столбом поравнялся «нос» поезда, до момента, когда со столбом поравнялся «хвост» поезда. За это время «нос» поезда успеет «уехать» на расстояние, равное длине поезда.

Таким образом, «Мимо семафора за 24сек» — это значит, что за 24сек поезд проходит расстояние, равное своей длине.

S = V ∙ t = lпоезда 

Ответ: 560 метров

Вывод: Время движения мимо неподвижной точки – это время, за которое длинный объект проходит расстояние, равное своей длине.

Поезд проезжает мост со скоростью 90 км/ч за 42 секунды. Какова длина поезда, если длина моста 634 метров?

«Проезжает мост за 42 сек» – это время от момента, когда на мост въезжает «нос» поезда, до момента, когда с моста съезжает «хвост» поезда. За это время «нос» поезда успеет «уехать» на расстояние, равное.

Таким образом, «Проезжает мост за 42 сек» – это значит, что за 42 сек поезд проходит расстояние, равное сумме длин моста и поезда. 

S = V ∙ t = l моста  lпоезда

l моста  lпоезда = 90 км/ч ∙ 42 сек = 1050 м;     lпоезда = 416 м

Ответ: длина поезда 416 метров

Вывод: Если длинный объект движется мимо неподвижного длинного объекта, то он проходит расстояние равное сумме длин обоих объектов

Какова длина поезда, успевающего проехать мимо идущего навстречу ему вдоль путей пешехода за 6 секунд, если скорость пешехода 4,2 км/ч, а скорость поезда 108 км/ч?

«Проехать мимо идущего навстречу пешехода за 6 секунд» — это время от момента, когда с пешеходом поравнялся «нос» поезда, до момента, когда с пешеходом поравнялся «хвост» поезда, то есть

от  и до .

Это равносильно задаче на встречное движение пешехода и хвоста. Между пешеходом и «хвостом» поезда расстояние, равное длине поезда, через 6 секунд хвост и пешеход встретятся. Каково расстояние между ними, если их скорости известны.

Тогда     (Vпоезда  Vпешехода)∙ t = Sобщее = lпоезда;

или lпоезда = Sобщее = Sпоезда   S пешехода

lпоезда = ( 108км/ч 4,2 км/ч) ∙ 6 сек = 187 м

Ответ: длина поезда 187 м

Вывод: Если длинный объект движется мимо идущего навстречу пешехода, то длина поезда равна сумме расстояний, пройденным пешеходом и поездом вместе.

Какова длина поезда, успевающего проехать мимо идущего вдоль путей в том же направлении пешехода за 30 секунд, если скорость пешехода 5,4 км/ч, а скорость поезда 123 км/ч?

«проехать мимо идущего в том же направлении пешехода за30 секунд» — это время от момента, когда с пешеходом поравнялся «нос» поезда, до момента, когда с пешеходом поравнялся «хвост» поезда, то есть это время

от и до .

Это равносильно задаче на движение в одном направлении пешехода и хвоста.  «Хвост» поезда начал догонять  пешехода, когда расстояние между ними было равно длине поезда, и через 30 секунд догнал пешехода. Каким было расстояние между ними, если их скорости известны.

Тогда     (Vпоезда – Vпешехода)∙ t = Sобщее = lпоезда;

или lпоезда = Sобщее = Sпоезда – S пешехода

lпоезда = ( 123 км/ч – 5,4 км/ч) ∙ 30 сек = 980 м

Ответ: длина поезда 980 м

Вывод: Если длинный объект движется мимо идущего в том же направлении пешехода, то длина поезда равна разности расстояний, пройденным поездом и пешеходом.

Две сороконожки проползали мимо друг друга 12 секунд. Скорость старшей из них 54 см/мин, а скорость младшей из них 61 см/мин. Какова длина младшей, если старшая к своим годам достигла 12 см.

«Проползали мимо друг друга 48 секунд» — это время между моментом, когда совместятся их носы, до момента, когда совместятся их хвосты. Другими словами, перед нами задача на встречное движение хвостов при исходном расстоянии, равном сумме длин сороконожек.

Тогда     (V1  V2)∙ t = Sобщее = l1   l2

l1   l2 = (54см/мин 69 см/мин) ∙ 48 сек = 23 см;    l2 = 11см

Ответ: длина младшей сороконожки 11 см.

Старый удав и резвый уж ползли к водопою. При этом уж, имея скорость 46 см/с, прополз мимо удава, длиной 8 метров, за 24 секунды. Какова длина ужа, если скорость удава 11 см/сек.

«Прополз мимо удава за 24 секунды» — это время от момента, когда нос ужа поравнялся с хвостом удава, до момента, когда хвост ужа поравнялся с носом удава, то есть это время за которое хвост ужа догонит нос удава, если расстояние между ними равно сумме их длин.

Тогда     (Vужа – Vудава)∙ t = Sобщее = l ужа  l удава ;

l ужа  l удава = (46 см/с – 11 см/с) ∙24 = 840 см; l ужа = 840 см – 8м = 40см

Ответ: длина ужа 40 см.

Возможны другие задачи, в которых сочетаются разные ситуации шести основных случаев, или иначе расставлены данные задачи и вопрос задач.

Электричка проходит мимо столба за 8 секунд. За какое время (в секундах) пройдут мимо друг друга пассажирский поезд и электричка, если скорость пассажирского поезда равна скорости электрички, а длина пассажирского поезда в полтора раза больше длины электрички?

Решение: 1). Пусть длина электрички а метров, тогда длина поезда 1,5а метра.

2). «Мимо столба за 8 сек» — это время от момента, когда со столбом поравнялся нос электрички, до момента, когда со столбом поравнялся хвост электрички, за это время нос электрички успел «уехать» на расстояние, равное длине электрички.

Таким образом,  «Мимо столба за 8 сек» — это значит, что за 8 сек электричка проходит расстояние, равное своей длине.

Тогда скорость электричкики (а/8) м/с, такая же скорость и у поезда.

3).»Пройдут мимо друг друга пассажирский поезд и электричка» — это время от момента, когда объекты «коснутся » носами, до момента, когда объекты «коснутся » хвостами. Перефразируем эту часть задачи:

Хвост электрички и хвост поезда начали двигаться навстречу друг другу, когда между ними было расстояние, равное сумме длин электрички и поезда. Через сколько секунд они встретятся, если их скорости равны и равны а/8?

Надо общее расстояние (а 1.5а) разделить на общую скорость (а/8 а/8), т.е. (2.5а)/(а/4)=20

Ответ: за 20 сек

Подъезжая к станции скорый поезд снизил скорость в момент, когда между кабиной машиниста и началом платформы было 320 метров, и через снова набрал её, когда между его хвостом и концом платформы стало 230 метров. С какой скоростью шёл скорый мимо платформы, если его длина 210 метров, а длина платформы 400 метров?

Решение:

 Vпоезда ∙t = Sпоезда = (320 400 230 210)м; Vпоезда =1160 м : 12 мин. = 5,8 км/ч

9.   Поезд длиной 240 метров мимо смотрителя прошёл за 12 секунд. Какова длина железнодорожного моста ( в км ), если на его прохождение поезд потратил 1 мин.   (  Ответ: 0.96 км  )

10. Найти скорость и длину поезда, зная, что он проходит мимо светофора за 7 секунд, и тратит 25 секунд на прохождение с той же скоростью вдоль платформы длиной 378 метров.    ( Ответ: 75,6 км/ч и 147 м  )

11.   Два поезда длиной 490 м и 210 м равномерно движутся навстречу друг другу по параллельным путям. Машинист одного из них заметил  встречный состав на расстоянии 700 м;  после этого через 28 секунд поезда встретились. Найти скорость каждого из них ( в км/ч ), если один из них проезжает мимо  светофора на 35 с дольше другого.  (  Ответ: 36 км/ч и 54 км/ч  )

12.   По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 160 метров, второй — длиной 140 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 300 метров. Через 9 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 900 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

13.   По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 140 метров, второй — длиной 60 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 800 метров. Через 15 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 1000 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

14.  Поезд, двигаясь равномерно со скоростью 183 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 3 км/ч, за 13 секунд. Найдите длину поезда в метрах.

15.  Три свечи имеют одинаковую длину, но разную толщину. Первая свеча была зажжена на 1 час раньше двух других, зажженных одновременно. В некоторый момент горения первая и третья свечи стали одной длины, а через 2 часа после этого одинаковой длины стали первая и вторая свечи. За сколько часов сгорает первая свеча, если вторая сгорает за 12 часов, а третья – за 8 часов?  ( Ответ: 16 часов  )

Роман Широбоков

Ученик

(150),
закрыт

9 месяцев назад

Задача: Свежие фрукты состоят на 86 % из воды, а сушёные — на 23 %. Сколько сушёных фруктов получится из 396 кг свежих?
Двумя способами решал её, но всё равно получалось 146,52 кг.
Первый способ у меня через нахождение процента потерь, а второй — через нахождение массы «мякоти», которая никак при сушке не могла исчезнуть, а потом находил массу воды из свежих фруктов при переходе в сушёные из 396 кг (т. е. просто 23 % от 396 кг), а потом просто прибавил массу «мякоти» к полученной оставшейся воде.
В итоге ответ всегда был 146,52 кг, если не ошибаюсь

АС идёт наxуй

Мыслитель

(5309)


11 месяцев назад

396 кг свежих содержат 396 * (100 — 86) / 100 = 55.44 кг мякоти
что составляет 100-23 = 77% от полной массы сушёных
тогда масса сушёных = 55.44 * 100 / 77 = 72 кг

Роман ШиробоковУченик (150)

11 месяцев назад

Спасибо! Просто смотрел в официальных источниках, но ничего так и не понял, откуда они вообще берут соотношения. Теперь понял)

© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Тесты

Автор Время чтения 5 мин.Просмотры 242Опубликовано 22.10.2019В данном разделе представлены все необходимые материалы для подготовки к ОГЭ по математике 2019. Мы предоставляем как разобранные варианты с теорией по заданиям

, так и тестовые варианты

для самоподготовки. Пройдя курс подготовки к ОГЭ на нашем сайте, вы уверенно напишете экзамен в 9 классе в 2020 году!

В связи со значительными изменениями в 2020 году в настоящий момент раздел перерабатывается!

Тематические задания с подробным решением

Модуль «Алгебра»

Задание №1 — числа и вычисления

Задание №2 — анализ диаграмм, таблиц, графиков

Задание №3 — числовые неравенства, координатная прямая

Задание №4 — алгебраические выражения

Задание №5 — анализ диаграмм, таблиц, графиков

Задание №6 — уравнения, неравенства и их системы

Задание №7 — простейшие текстовые задачи

Задание №8 — анализ диаграмм и графиков

Задание №9 — статистика и вероятности

Задание №10 — сопоставление графиков функций

Задание №11 — арифметические и геометрические прогрессии

Задание №12 — алгебраические выражения

Задание №13 — расчеты по формулам, подстановка

Задание №14 — уравнения, неравенства и их системы

Модуль «Геометрия»

Задание №15 — практические задачи по геометрии

Задание №16 — треугольники, четырёхугольники, многоугольники

Задание №17 — окружность, круг и их элементы

Задание №18 — площади различных фигур

Задание №19 — фигуры на квадратной решетке

Задание №20 — анализ геометрических высказываний

Вторая часть

Задание №21 — решение уравнений

Задание №22 — текстовая задача

Задание №23 — график функции

Задание №24 — треугольники

Задание №25 — четырехугольники

Задание №26 — «сложная» геометрияБал

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

2

2

2

2

2

2

Сложность

♦
◊◊

♦
◊◊

♦
◊◊

♦
◊◊

Тест

Тест №1

Тест №2

Тест №3

Тест №4

Тест №5

Тест №6

Тест №7

Тест №8

Тест №9

Тест №10

Тест №11

Тест №12

Тест №13

Тест №14

Тест №15

Тест №16

Тест №17

Тест №18

Тест №19

Тест №20Как правильно пройти подготовку к тестам ОГЭ в 9 классе?

Многие учащиеся задаются этим вопросом и каждый год я объясняю новым школьникам как правильно готовиться к экзаменам ОГЭ и получить отличную отметку. Накопленный мною опыт в подготовке учеников к итоговой аттестации в 9 классе по математике собран в данном разделе и постоянно пополняется.Как пользоваться этим разделом?

Все задания в тематические, то есть каждый номер проверяет какие-то конкретные знания из области курса математики. На каждой кнопке, ведущей к разбору задания написана тема данного номера. Вы выбираете номер задания, который вас интересует и попадаете на страницу с подробным разбором, примерами решения и объяснениями. Важно отметить, что я не просто решаю задания, но и даю теоретические справки по общему подходу к решениям таких заданий. После разбора одного из разделов вы будете готовы решить любое задание из ОГЭ по математике.Материалы и пособия для подготовки 2019

Демонстрационный вариант 
Разборы ОГЭ по другим предметам:

Последним рубежом школьных экзаменов уже давно считают ОГЭ – экзамен, который проверяет знание учеников девятых классов. Несмотря на относительно низкий процент будущих студентов учебных заведений I-II уровня аккредитации, подобный тест все же определяет уровень знаний. Результат может повлиять на получение медали, при поступлении в ВУЗ. Потому, сайт Фипи информирует про ОГЭ 2017 года, и предоставляет необходимые данные для предварительной подготовки.

Как подготовиться к ОГЭ при помощи сайта ФИПИ?

Зайдя на нужную вкладку, можно найти общую информацию об ЕГЭ и ОГЭ. Это терминологические обозначение обоих экзаменов, все необходимые предметы и направления, что могут понадобиться при сдаче.

Сайт Фипи

Все, что требуется знать ученикам об экзамене, рассказывает сайт ФИПИ ОГЭ 2017 года – немного отличается от того, что было в предыдущем году. Сам сайт полностью направлен на подготовку и ознакомление учеников средне образовательных школ. Чтобы детальней вникнуть во все нюансы, стоит рассмотреть все ссылки, предоставляемые специалистами учащимся и их родителям.

Далее удобно будет перейти во вкладку «Открытый банк заданий».

Банк заданий ОГЭ на ФИПИ

Здесь предоставлены задания по основным экзаменационным тестам:

• филологическое направление родного языка;
• иностранные языки согласно рекомендациям учебного заведения;
• точные науки;
• естественные науки;
• технические предметы

Переход по каждой вкладке сайта ФИПИ касательно ОГЭ 2017 года подразумевает развернутое тестирование на каждый предмет.

Банк заданий на ФИПИ по русскому

Здесь каждый ученик может предварительно ознакомиться с формой и подачей каждого задания.

Кроме того, удобное разделение на подразделы и темы позволит упростить непосредственную подготовку к экзамену. Это позволит правильно распланировать время, которое осталось к итоговому экзамену после окончания 9 класса.

Дополнительные ссылки и помощь специалистов

Одной и важных функций на страничке портала является «Переговорная». Нажатие на иконку вызывает поля для ввода данных.

Переговорная

Таким образом, можно попасть в виртуальную комнату, где задаются вопросы и озвучиваются ответы на них. В режиме живого общения можно уточнить все интересующие детали, разузнать моменты, которые оказались непонятными.

Кроме информации о предстоящем экзамене, сайт ФИПИ для ОГЭ 2017 года предлагает практическую помощь. Например, будет полезна рубрика «Итоговое сочинение».

Итоговое сочинение

Это задание направлено на практическую проверку знаний языка у каждого ученика. И чтобы детальней подготовиться к выкладке тематики, спланировать ход мыслей, предлагается ознакомиться со всеми «подводными камнями» этого раздела в экзамене.

—>

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?

Источник: Банк заданий ФИПИ

---

2

При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?

Источник: Банк заданий ФИПИ

---

3

Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?

Источник: Банк заданий ФИПИ

---

4

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

---

5

Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.

Пройти тестирование по этим заданиямзадача про фрукты

ОГЭ № 22 Задачи на процентное содержание

Тимофеева Марина Николаевна – учитель математики

Задачи на процентное содержание

Задачи с растворами

Задачи с фруктами…

Задачи со сплавами

Задачи с фруктами Надо знать: 1% = 0,01 Часть от числа находится умножением Масса сухой составляющей остаётся неизменной 1. Свежие фрукты содержат 80% воды, а высушенные — 4%. Сколько требуется свежих фруктов для приготовления 2 кг высушенных фруктов?

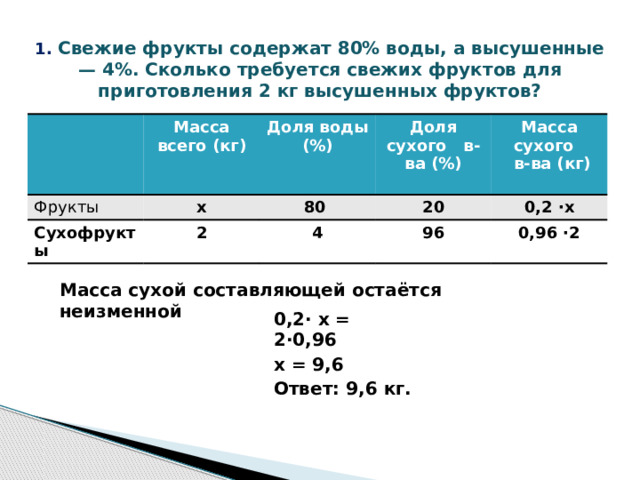
1. Свежие фрукты содержат 80% воды, а высушенные — 4%. Сколько требуется свежих фруктов для приготовления 2 кг высушенных фруктов?

Масса всего (кг)

Фрукты

х

Доля воды (%)

Сухофрукты

Доля сухого в-ва (%)

2

80

Масса сухого

20

4

96

в-ва (кг)

0,2 ·х

0,96 ·2

Масса сухой составляющей остаётся неизменной

0,2· x = 2·0,96

х = 9,6

Ответ: 9,6 кг.

Самостоятельная работа

2.1 Свежие фрукты содержат 75% воды, а высушенные – 25%. Сколько требуется свежих фруктов для приготовления 45 кг высушенных фруктов?

2.2 Свежие фрукты содержат 72% воды, а высушенные – 20%. Сколько сухих фруктов получится из 100 кг свежих фруктов?

2.3 Сколько килограммов сухарей влажностью 25% можно получить из 225 кг хлеба влажностью 45%.

Ответы: 1) 135 кг; 2) 35 кг; 3) 165 кг.

Тренировочные упражнения

Ответы: 4.1.105. 420 кг; 4.1.106. 90 кг.

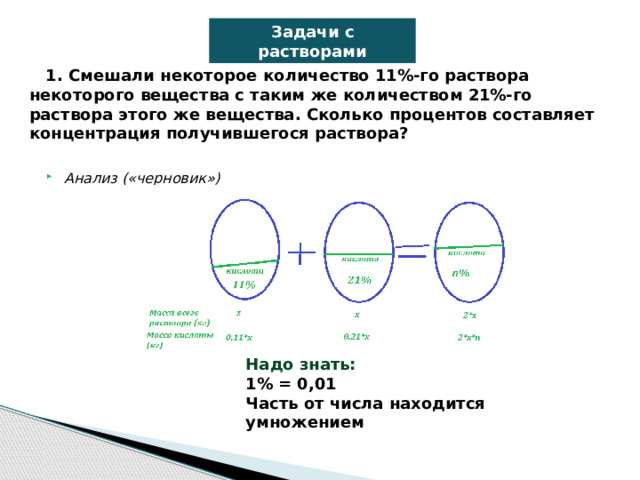
Задачи с растворами

1. Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 21%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

• Анализ («черновик»)

Надо знать: 1% = 0,01 Часть от числа находится умножением

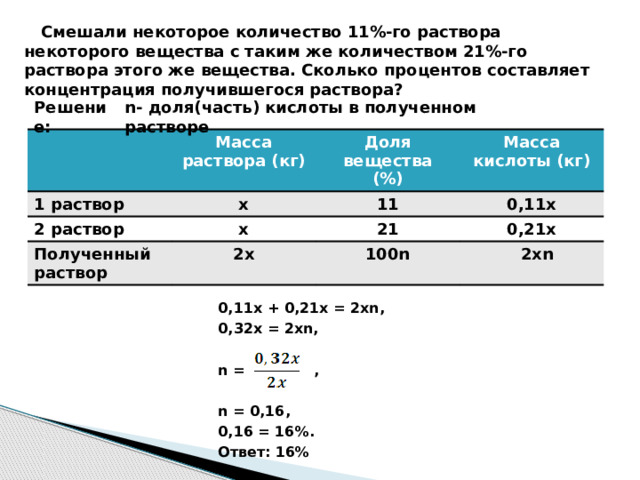
Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 21%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

n- доля(часть) кислоты в полученном растворе

Решение:

Масса раствора (кг)

1 раствор

x

2 раствор

Доля вещества

11

x

Полученный раствор

(%)

Масса кислоты (кг)

2x

0,11x

21

0,21x

100n

2xn

0,11x 0,21x = 2xn,

0,32x = 2xn,

n = ,

n = 0,16,

0,16 = 16%.

Ответ: 16%

2. Имеются два сосуда, содержащие 20 и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 41% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 43% кислоты. Сколько килограммов кислоты содержится в первом растворе?

Анализ («черновик»)

Надо знать: 1% = 0,01 Часть от числа находится умножением

= 0,8

Имеются два сосуда, содержащие 20 и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 41% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 43% кислоты. Сколько килограммов кислоты содержится в первом растворе?

Решение:

1 раствор

Масса всего раствора (кг)

20

2 раствор

Доля кислоты

Масса кислоты (кг)

16

Вместе

(%)

x

36

y

41

0,41∙ 36

Масса всего раствора (кг)

1 раствор

2 раствор

Доля кислоты

16

Вместе

Масса кислоты (кг)

16

(%)

0,8 ∙ x

32

y

43

0,43 ∙ 32

х y = 0,41 ∙ 36,

0,8x y = 0,43 ∙ 3;

х = 5.

Ответ: 5 кг.

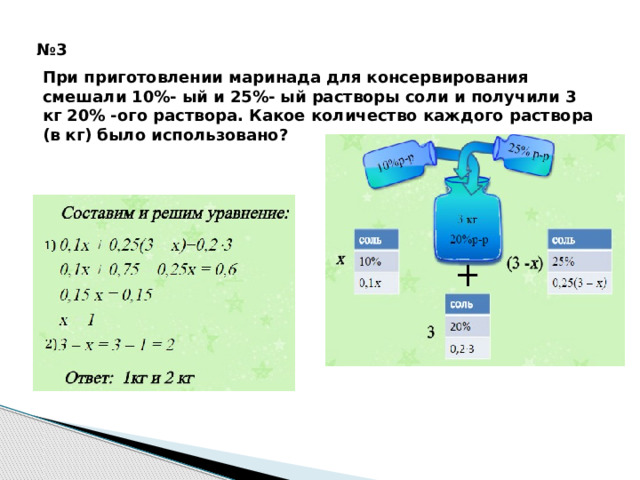
№ 3

При приготовлении маринада для консервирования смешали 10%- ый и 25%- ый растворы соли и получили 3 кг 20% -ого раствора. Какое количество каждого раствора (в кг) было использовано? 

Самостоятельная работа

2.1. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получился раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?

2.2. Имеются два сосуда, содержащих 4 кг и 6 кг раствора кислоты разных концентраций. Если их слить вместе, то получится раствор, содержащий 35% кислоты. Если же слить равные массы этих растворов, то получится раствор, содержащий 36% кислоты. Сколько кг кислоты содержится в каждом сосуде?

Ответы: 1) 2 : 1; 2) 1,64 кг, 1,86 кг.

Тренировочные упражнения

Ответы: 4.1.103. 2:1; 4.1.104. 2:1; 4.1.141. 15,6 кг; 4.1.142. 2,6 кг.

Задачи со сплавами

№ 1

= ?

Источники

• http://www.myshared.ru/slide/1100817 /
• http:// matem-kovalenko.ucoz.ru/load/prezentacii_k_urokam/zadachi_na_procenty_zadanija_22_ogeh/2-1-0-7
• http:// www.uchportal.ru/video/vic/ogeh_gia_po_matematike/zadacha_22
• http://dmou7.edumsko.ru/collective/pedagogical_collective/moskevich_larisa_vyacheslavovna/materials/materialy_k_uroku_matematiki/podgotovka_k_oge_zadacha_22 /

А. В. Семёнов, А. С. Трепалин, И. В. Ященко, П. И. Захаров, И. Р. Высоцкий. Математика . ФИПИ. Комплекс материалов для подготовки учащихся, ОГЭ 2016. Москва «Интеллект-Центр» 2016 Очень интересное мероприятие прошло 25 мая в МБОУ"Тархан-Потьминская ООШ" по математике. Было все подготовлено основательно. Очень много было интересного оборудования. Учащиеся и все присутствующие остались довольными и благодарили учителя математики за проведенное мероприятие.